[专业知识001] 算法设计与分析
算法时间复杂度
Get the knowledge flowing and circulating! :)
目录
算法 & 算法复杂度
算法是解决某个问题的计算方法和步骤,是一个计算过程,这个过程中会包括一系列解决问题的清晰指令。
算法复杂度是指算法在编写成可执行程序后运行时所需要的时间资源和内存资源。程序的时间开销和内存开销分别使用时间复杂度和空间复杂度描述。
时间复杂度
概念
一般来说,时间复杂度是一个关于问题规模
例1:在计算

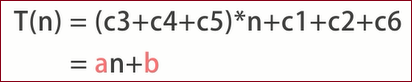
T(n)是n的一次函数
例2:代码功能是

T(n)是n的二次函数
在大多数情况下,分析算法的时候,我们并不需要精确的计算出
分析方法
所以,通常情况,我们在研究某个算法时,输入的时间规模
:代表时间复杂度的渐进上界
:代表时间复杂度的渐进下界
:代表时间复杂度的渐进确界
已知
如果对于任意
比方说,
存在
对于任意
如果
对于大部分的算法分析,我们只需要关注算法的渐进上界,即,使用
这是因为,大家在使用算法的时候,几乎不会考虑下界
的,因为如果人们说,请设计一个 的算法,大家希望得到的算法满足最坏情况下不超过 ,如果这个时候设计出一个 的算法,肯定也是满足需求的。人们也不会表达说,需要 但不需要 的算法;这种情况换一种说法,当人们说,这种算法是 的时候,希望表达的是这个算法至少是 ,不会比 差(比如, )。
算法时间复杂度排序:
总结 所以,我们在分析算法时间复杂度的时候,能够将算法使用
例如:在下面这段代码中,c1, c2, c9都是常量级执行时间;c3, c4, c8对应


虽然说,代码千差万别,但是常见的时间复杂度并不多。↓
常见算法时间复杂度
通常情况下,这些算法时间复杂度可以覆盖全部面试中可能碰到的问题的时间复杂度
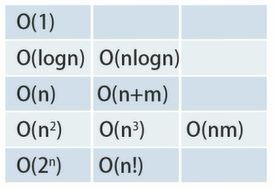
常量复杂度
很多经典的算法都是对数时间,例如二分查找、快速排序、二叉搜索树等等。
例如:在下面这段代码中,累加1、2、4、8...一直到

对于
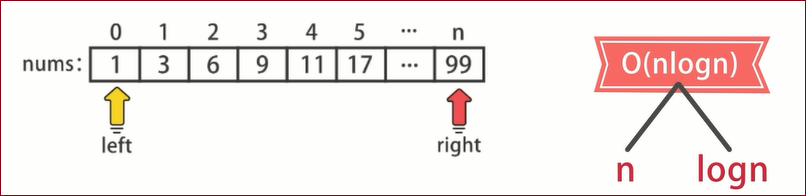
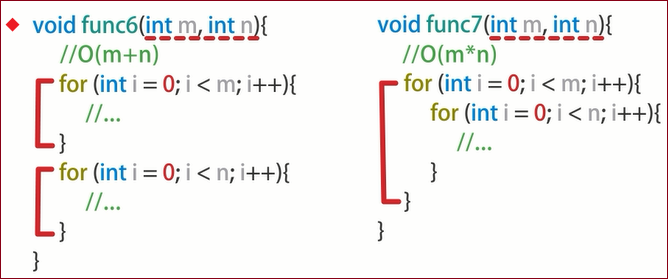
▲对于

◆而如果输入数据有两个变量,就会出现
对于指数级和阶乘时间复杂度,一般为
这种非多项式量级的算法问题被称为NP问题,也就是
Non-Deterministic Polynomial(非确定多项式问题)。当数据规模
所以非多项式时间复杂度的算法是非常低效的。暴力回溯法可能会出现
deterministic
美/ dɪˌtɜːrmɪˈnɪstɪk /adj.确定性的;命运注定论的The rise or decline of the United States is not a function of deterministic forces.
美国的兴衰不是不可抗拒力的作用。
non-deterministic
adj.非确定的
n.不确定性;非决定性
Works by capturing, recording and replaying non-deterministic events and inputs.
通过捕获、记录和重现非决定性的时间和输入而工作。
polynomial
美/ ˌpɑːliˈnoʊmiəl /adj.多项的,多词的;多项式的
n.多项式;多词拉丁学名;表示任何多项数之和
Based on the relationship between the group delay function and the cepstral coefficients, the denominator polynomial coefficients can be determined.
根据群延迟函数与倒谱系数之间的关系,可以确定分母的多项式系数。
总结来说,经典算法中最常出现的算法复杂度是
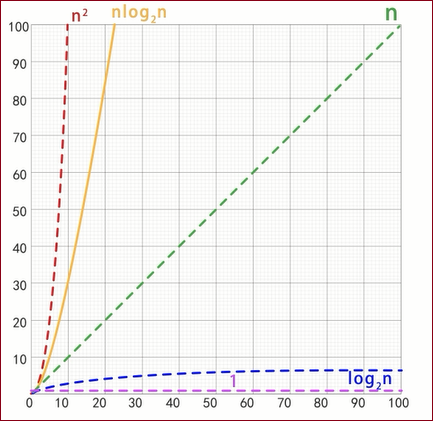
常见的5种算法时间复杂度